描述
在一个排列中,如果一对数的前后位置与大小顺序相反,即前面的数大于后面的数,那么它们就称为一个逆序。一个排列中逆序的总数就称为这个排列的逆序数。
思路
暴力出奇迹
- 对于每一个数都遍历一遍排在他前面的数,每有一个比他大的数就ans++,时间复杂度为$O(n^2)$,很明显这个算法只能应用于数很少的情况。
归并排序求逆序数
- 归并排序中,在每次合并的时候判断一下。
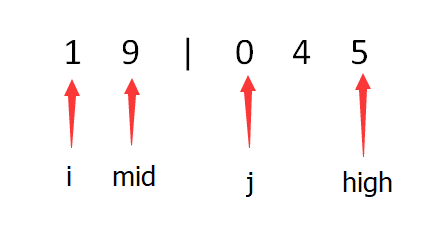
- 假设数列为9 1 0 5 4,先把它分成两个子序列,9 1 | 0 5 4,使左右分别有序,则有1 9 | 0 4 5,此时进行两个子序列合并。如果a[i]<=a[j],则i++,继续比较,如果a[i]>a[i],则说明a[i]到a[mid]的数都大于a[j],那么ans+=mid-i+1。
代码
1 | ll a[500005],tem[500005],ans; //a为要求的序列,tem是临时存放的数组 |
用树状数组求逆序数
- 这个算法的思想就是依次插入序列的数,每插入一个就ans+=在这个数前面比它大的数的个数。最后的ans就是答案。
- 用一个数组tr[x],tr[x]=1代表x在序列中存在1个。一开始tr都为0,因为此时未插入任何数。
- 此时的树状数组tr[x]代表在x前lowbit(x)个数有多少个数比它小。
- 初始化tr数组为0,代表一开始所有数都没有插入。
- 每次插入一个数x就是tr[x]++,再更新一次树状数组,维护区间和。
离散化处理
- 根据上面的思路,我们很容易发现我们要开很大的数组。如果题目说长度为$5 \times 10^5$数列a中$a_i \leq 10^9$,这时候开$10^9$的数组就太浪费了,我们就可以离散化处理。
- 我们离散化的目的就是为了把$10^9$的数对应到$5 \times 10^5$中,举个例子:
原序列为: 999 23 0 98765 2 7
离散化后: 5 4 1 6 2 3
说白了就是用一个$1-n$的数列来代替原序列,而逆序数不变。- 没看懂的可以跟着代码模拟一遍。
代码
1 |
|