描述
传送门:poj-2528
一样的题:swustoj-764(校门外的树 Plus Plus)
The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election campaign have been placing their electoral posters at all places at their whim. The city council has finally decided to build an electoral wall for placing the posters and introduce the following rules:
- Every candidate can place exactly one poster on the wall.
- All posters are of the same height equal to the height of the wall; the width of a poster can be any integer number of bytes (byte is the unit of length in Bytetown).
- The wall is divided into segments and the width of each segment is one byte.
- Each poster must completely cover a contiguous number of wall segments.
They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections.
Your task is to find the number of visible posters when all the posters are placed given the information about posters’ size, their place and order of placement on the electoral wall.
Input
The first line of input contains a number c giving the number of cases that follow. The first line of data for a single case contains number $1\ <=\ n\ <=\ 10000$. The subsequent n lines describe the posters in the order in which they were placed. The $i^{th}$ line among the n lines contains two integer numbers $l_i$ and $r_i$ which are the number of the wall segment occupied by the left end and the right end of the $i^{th}$ poster, respectively. We know that for each $1\ <=\ i\ <=\ n$, $1 <= l_i <= r_i <= 10000000$. After the $i^{th}$ poster is placed, it entirely covers all wall segments numbered $l_i, l_{i+1} ,… , r_i$.
Output
For each input data set print the number of visible posters after all the posters are placed.
The picture below illustrates the case of the sample input.
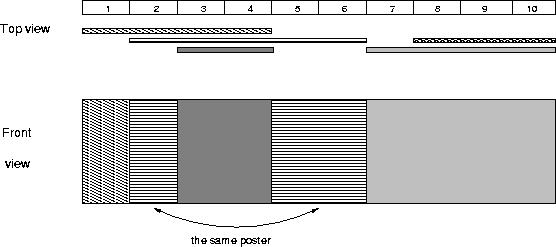
Examples
- intput
1 | 1 |
- output
1 | 4 |
题目大意
有$n$张海报要贴到墙上,按张贴顺序给出了每张海报贴的起始位置(只考虑横坐标),求最后能看到的海报的数量(只要有一点能看到就算能看到)。
思路
- 很明显要用线段树,维护区间是否被覆盖了。
- 我们可以很显然想到,应该倒序覆盖区间,因为最后面贴的一定是看得到的。
- 每次覆盖的时候判断是否需要更新区间的状态。也就是说,如果你即将覆盖的区域已经(由于之前的覆盖操作)完全被覆盖了,那么就不需要更新这个区间的状态了。相当于是你现在要贴的海报会被后面要贴的海报所完全覆盖,那么你现在要贴的这张海报最后就看不到了。
- 每次覆盖的时候,如果需要更新区间,那么ans++,详见代码。
代码
1 |
|

